一.向前计算
对于pytorch中的每个tensor,如果设置它的属性.requires_grad为True,那么它将追踪对于该张量的所有操作。或者可以理解为,这个tensor是一个参数,后续会被计算梯度,更新该参数。
tensor(data,requires_grad=True)
1.计算过程
import torch
# 初始化参数x
x = torch.ones(2, 2, requires_grad=True)
# requires_grad=True用来追踪其计算历史
print(x)
#tensor([[1., 1.],
# [1., 1.]], requires_grad=True)
y = x + 1
print(y)
# tensor([[2., 2.],
# [2., 2.]], grad_fn=<AddBackward0>)
# 平方乘2
z = y*y*2
print(z)
# tensor([[8., 8.],
# [8., 8.]], grad_fn=<MulBackward0>)
# 求均值
out = z.mean()
print(out)
# tensor(8., grad_fn=<MeanBackward0>)
从上述代码可以看到:
1.x的requires_grad属性为True
2.之后的每次计算都会修改其grad_fn属性,用来记录做过的操作
2.requires_grad和grad_fn
import torch
a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad) # False
a.requires_grad = True
print(a.requires_grad) # 修改为True
b = (a * a).sum()
print(b.grad_fn) # <SumBackward0 object at 0x000001C102085A90>
with torch.no_grad():
c = (a * a).sum() # tensor(179.5280) 此时c没有grad_fn
print(c) # False
为了防止跟踪历史记录(和使用内存),可以将代码块包装在with torch.no_grad(): 中,在评估模型时特别有用。因为模型可能具有requires_grad = True的可训练参数,但是我们在评估的时候不需要对他们进行梯度计算。
二.梯度运算
1.可以使用backward方法来进行反向传播,计算梯度out.backward()。
反向传播:output.backward()
获取梯度:x.grad,累加梯度
- 每次反向传播之前,需要先把梯度置为0之后
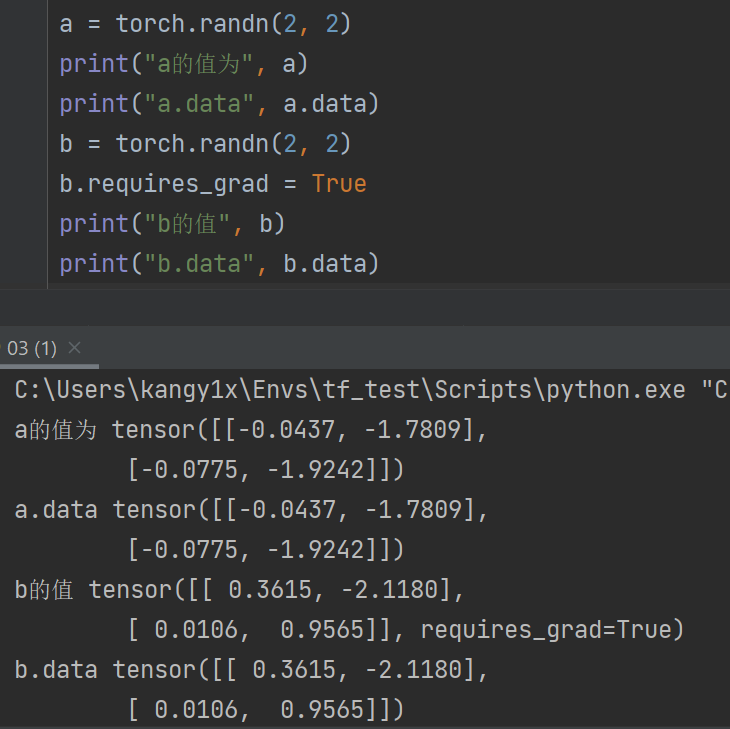
2.tensor.data
在tensor的require_grad=False,tensor.data和tensor等价
require_grad=True时,tensor.data仅仅获取tensor中的数据
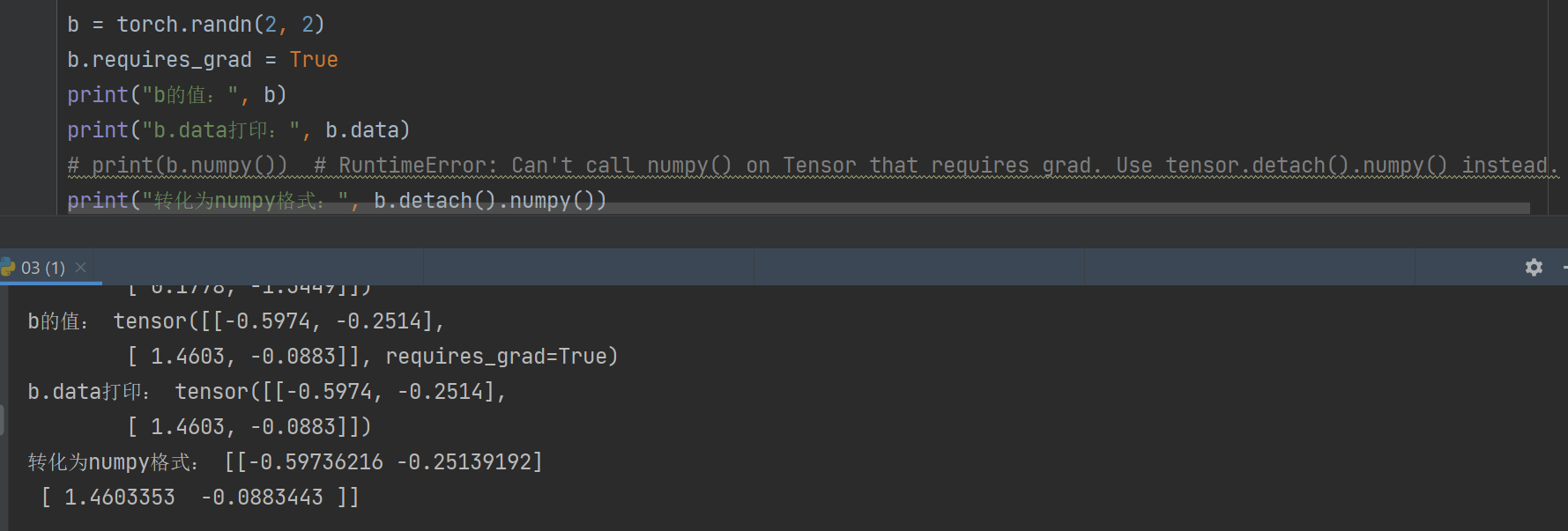
3.tensor.numpy()
当require_grad=True时不能够直接转换,需要使用tensor.detach().numpy(),可以实现对tensor中数据的深拷贝,转化为ndarray类型
三.手动实现线性回归
假设基础模型为y = wx + b,其中w和b均为参数,我们使用y = 3x + 0.8来构造数据x、y,所以最后通过模型应该能够得出w和b应该分别接近3和0.8
1.准备数据
2.计算预测值
3.计算损失,把参数的梯度置为0,进行反向传播
4.更新参数
代码演示:
import torch
import numpy as np
import matplotlib.pyplot as plt
learning_rate = 0.01
# 准备数据y = 3*x + 0.8
x = torch.rand([500, 1])
y = 3 * x + 0.8
# print(x, y)
# 通过模型计算y_predict
w = torch.rand([1, 1], requires_grad=True)
b = torch.tensor(0, requires_grad=True, dtype=float)
# 通过循环,反向传播,更新参数
for i in range(2000):
# 预测值
y_predict = torch.matmul(x, w) + b
# 计算loss,均方误差 pow(2)代表平方
loss = (y - y_predict).pow(2).mean()
# 判断梯度是否为0,非0要置为0,避免梯度累加
if w.grad is not None:
# 归0操作,就地修改
w.grad.data.zero_()
if b.grad is not None:
b.grad.data.zero_()
# 反向传播
loss.backward()
# 更新w和b
w.data = w.data - learning_rate * w.grad
b.data = b.data - learning_rate * b.grad
print("w,b,loss", w.item(), b.item(), loss.item())
# 画图
plt.figure(figsize=(13, 6))
plt.scatter(x.numpy().reshape(-1), y.numpy().reshape(-1))
y_predict = torch.matmul(x, w) + b
plt.plot(x.numpy().reshape(-1), y_predict.detach().numpy().reshape(-1))
plt.show()
图形效果如下:
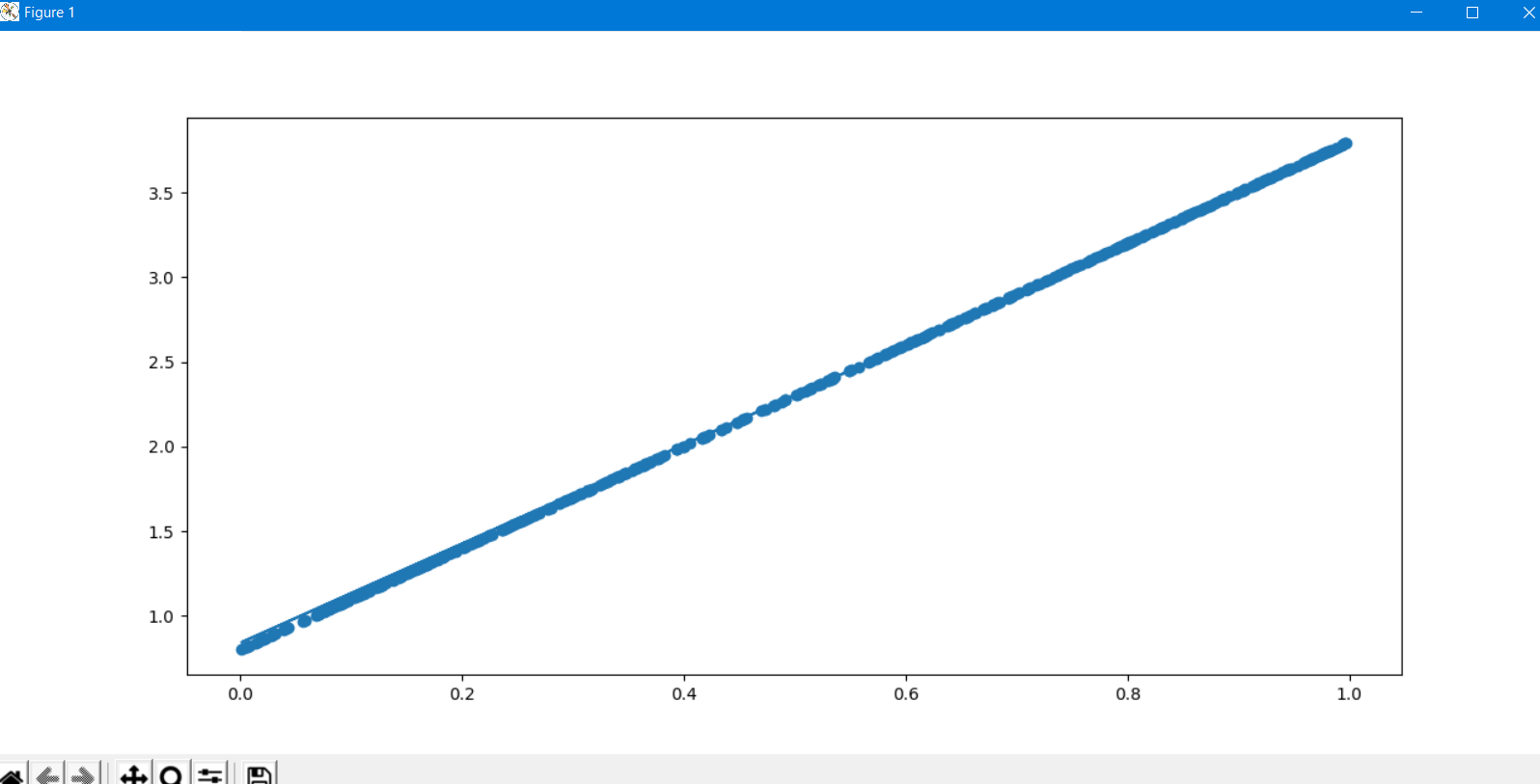
打印w,b和loss,可以看到w和b已经非常接近原理设定的3和0.8

