一.神经网络介绍
1.什么是神经网络
神经网络就是一个”万能的模型+误差修正函数“,每次根据训练得到的结果与预想结果进行误差分析,进而修改权值和阈值,一步一步得到能输出和预想结果一致的模型。
举一个例子: 比如某厂商生产一种产品,投放到市场之后得到了消费者的反馈,根据消费者的反馈,厂商对产品进一步升级,优化,从而生产出让消费者更满意的产品。这就是神经网络的核心。
2.神经网络的本质
机器学习可以看做是数理统计的一个应用,在数理统计中一个常见的任务就是拟合,也就是给定一些样本点,用合适的曲线揭示这些样本点随着自变量的变化关系。
深度学习同样也是为了这个目的,只不过此时,样本点不再限定为(x, y)点对,而可以是由向量、矩阵等等组成的广义点对(X,Y)。而此时,(X,Y)之间的关系也变得十分复杂,不太可能用一个简单函数表示。然而,人们发现可以用多层神经网络来表示这样的关系,而多层神经网络的本质就是一个多层复合的函数。
说白了,深度学习就是弄出来一个超级大的函数,这个函数含有海量的权值参数、偏置参数,再通过一系列复合的复杂运算,得到结果。
3.神经网络训练的基本思想
神经网络训练的最基本的思想就是:
| 先“猜”一个结果,我们叫预测结果a,看看这个预测结果和事先标记好的训练集中的真实结果y之间的差距,然后调整策略,再试一次,这一次就不是“猜”了,而是有依据地向正确的方向靠近。如此反复多次,一直到预测结果和真实结果之间相差无几,亦即 | a-y | ->0,就结束训练。 |
在神经网络训练中,我们把“猜”叫做初始化,可以随机,也可以根据以前的经验给定初始值。即使是“猜”,也是有技术含量的。
4.举例说明1

5.举例说明2
小明拿了一支步枪,射击100米外的靶子。这支步枪没有准星,或者是准星有问题,或者是小明眼神儿不好看不清靶子,或者是雾很大,或者风很大,或者由于木星的影响而侧向引力场异常……反正就是遇到各种干扰因素。
第一次试枪后,拉回靶子一看,弹着点偏左了,于是在第二次试枪时,小明就会有意识地向右侧偏几毫米,再看靶子上的弹着点,如此反复几次,小明就会掌握这支步枪的脾气了。下图显示了小明的5次试枪过程。
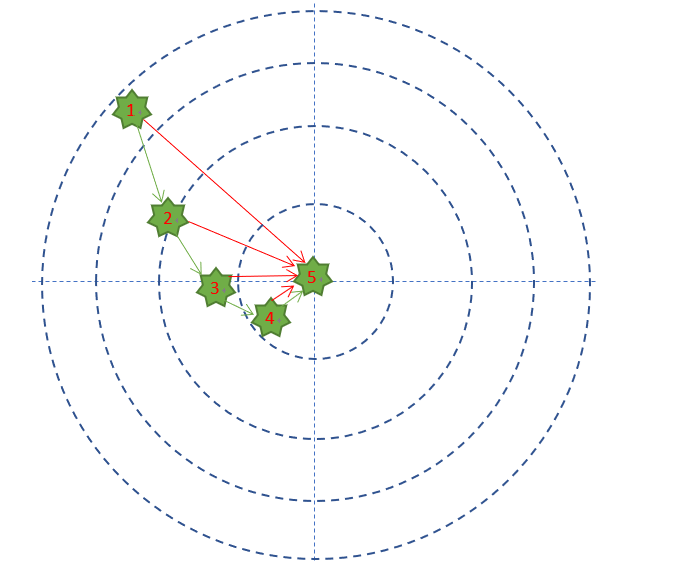
在有监督的学习中,需要衡量神经网络输出和所预期的输出之间的差异大小。这种误差函数需要能够反映出当前网络输出和实际结果之间一种量化之后的不一致程度,也就是说函数值越大,反映出模型预测的结果越不准确。
这个例子中,小明预期的目标是全部命中靶子的中心,最外圈是1分,之后越向靶子中心分数是2,3,4分,正中靶心可以得10分。
- 每次试枪弹着点和靶心之间的差距就叫做误差,可以用一个误差函数来表示,比如差距的绝对值,如图中的红色线。
- 一共试枪5次,就是迭代/训练了5次的过程 。
- 每次试枪后,把靶子拉回来看弹着点,然后调整下一次的射击角度的过程,叫做反向传播。注意,把靶子拉回来看和跑到靶子前面去看有本质的区别,后者容易有生命危险,因为还有别的射击者。一个不恰当的比喻是,在数学概念中,人跑到靶子前面去看,叫做正向微分;把靶子拉回来看,叫做反向微分。
- 每次调整角度的数值和方向,叫做梯度。比如向右侧调整1毫米,或者向左下方调整2毫米。如图中的绿色矢量线。 上图是每次单发点射,所以每次训练样本的个数是1。在实际的神经网络训练中,通常需要多个样本,做批量训练,以避免单个样本本身采样时带来的误差。在本例中,多个样本可以描述为连发射击,假设一次可以连打3发子弹,每次的离散程度都类似,如下图所示。
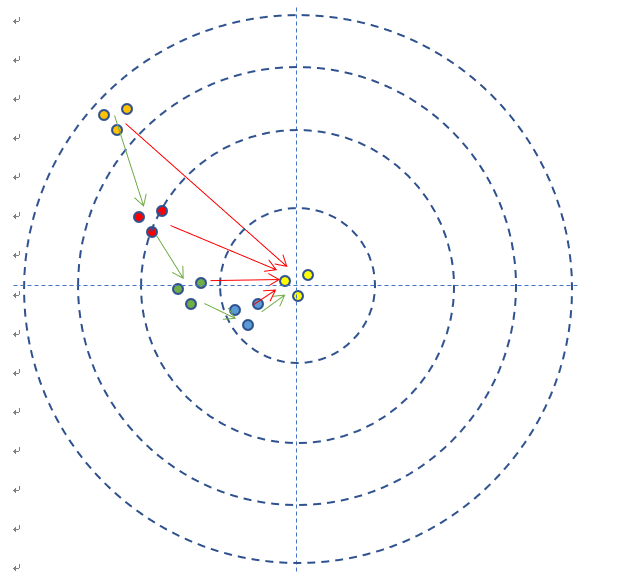
- 如果每次3发子弹连发,这3发子弹的弹着点和靶心之间的差距之和再除以3,叫做损失,可以用损失函数来表示。
那小明每次射击结果和目标之间的差距是多少呢?在这个例子里面,用得分来衡量的话,就是说小明得到的反馈结果从差9分,到差8分,到差2分,到差1分,到差0分,这就是用一种量化的结果来表示小明的射击结果和目标之间差距的方式。也就是误差函数的作用。因为是一次只有一个样本,所以这里采用的是误差函数的称呼。如果一次有多个样本,就要叫做损失函数了。
其实射击还不这么简单,如果是远距离狙击,还要考虑空气阻力和风速,在神经网络里,空气阻力和风速可以对应到隐藏层的概念上。-
在这个例子中:
- 目的:打中靶心;
- 初始化:随便打一枪,能上靶就行,但是要记住当时的步枪的姿态;
- 前向计算:让子弹飞一会儿,击中靶子;
- 损失函数:环数,偏离角度;
- 反向传播:把靶子拉回来看;
- 梯度下降:根据本次的偏差,调整步枪的射击角度,goto前向计算。
损失函数的描述是这样的:
1环,偏左上45度; 6环,偏左上15度; 7环,偏左; 8环,偏左下15度; 10环。
这里的损失函数也有两个信息:
距离;
方向。
所以,梯度,是个矢量! 它应该即告诉我们方向,又告诉我们数值。
二.梯度下降的介绍
1.什么是梯度
是一个向量,导数+变化最快的方向(学习的前进方向)
梯度就是多元函数参数的变化趋势(参数学习的方向),只有一个自变量时称为导数。
2.为什么用梯度下降?
由浅入深,我们最容易想到的调整参数(权重和偏置)是穷举。即取遍参数的所有可能取值,比较在不同取值情况下得到的损失函数的值,即可得到使损失函数取值最小时的参数值。然而这种方法显然是不可取的。因为在深度神经网络中,参数的数量是一个可怕的数字,动辄上万,十几万。并且,其取值有时是十分灵活的,甚至精确到小数点后若干位。若使用穷举法,将会造成一个几乎不可能实现的计算量。
第二个想到的方法就是微分求导。通过将损失函数进行全微分,取全微分方程为零或较小的点,即可得到理想参数。(补充:损失函数取下凸函数,才能使得此方法可行。现实中选取的各种损失函数大多也正是如此。)可面对神经网络中庞大的参数总量,纯数学方法几乎是不可能直接得到微分零点的。
因此我们使用了梯度下降法。既然无法直接获得该点,那么我们就想要一步一步逼近该点。一个常见的形象理解是,爬山时一步一步朝着坡度最陡的山坡往下,即可到达山谷最底部。(至于为何不能闪现到谷底,原因是参数数量庞大,表达式复杂,无法直接计算)我们都知道,向量场的梯度指向的方向是其函数值上升最快的方向,也即其反方向是下降最快的方向。计算梯度的方式就是求偏导。
这里需要引入一个步长的概念。此梯度对参数当前一轮学习的影响程度。步长越大,此梯度影响越大。若以平面直角坐标系中的函数举例,若初始参数x=10,步长为1 。那么参数需要调整十次才能到达谷底。若步长为5,则只需2次。若为步长为11,则永远无法到达真正的谷底。
三. 反向传播
损失函数为我们提供了计算损失的方法;
梯度下降是在损失函数基础上向着损失最小的点靠近而指引了网络权重调整的方向,是找损失函数极小值的一种方法
反向传播把损失值反向传给神经网络的每一层,让每一层都根据损失值反向调整权重,是求解梯度的一种方法
前向传递输入信号直至输出产生误差,反向传播误差信息更新权重矩阵。其根本就是求偏导以及高数中的链式法则
1.案例:

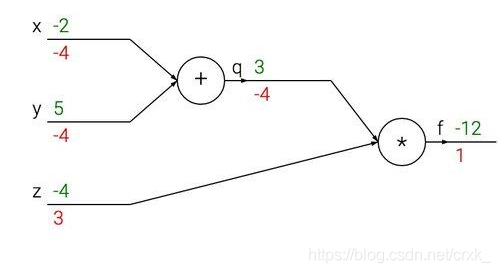
四.损失函数介绍
在训练阶段,深度神经网络经过前向传播之后,得到的预测值与先前给出真实值之间存在差距。我们可以使用损失函数来体现这种差距。损失函数的作用可以理解为:当前向传播得到的预测值与真实值接近时,取较小值。反之取值增大。并且,损失函数应是以参数(w 权重, b 偏置)为自变量的函数。
五.如何训练神经网络
训练神经网络,“训练”的含义:
它是指通过输入大量训练数据,使得神经网络中的各参数(w 权重, b 偏置)不断调整“学习”到一个合适的值。使得损失函数最小。
如何训练?
采用 梯度下降 的方式,一点点地调整参数,找损失函数的极小值(最小值)
线性与非线性反向传播可以参看下文资料:
