一.线性回归（Linear regression）概述

1.定义

是利用回归方程（函数）对一个或多个自变量（特征值）和因变量（目标值）之间关系进行建模的一种分析方式。

2.特点

只有一个自变量的情况称为单变量回归，多余一个自变量的情况叫做多元回归。

3.公式

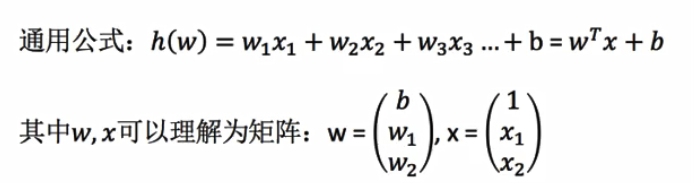
4.分类：

• 线性关系
  • 单变量线性关系
  • 多变量线性关系
• 非线性关系

二.线性回归API初步使用

1.线性回归api

2.代码演示

# 导入模块
from sklearn.linear_model import LinearRegression

# 构造数据集
x = [[80, 86], [82, 80], [85, 78], [90, 90], [86, 82], [82, 90], [78, 80], [92, 94]]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]

# 模型训练
# 实例化API
estimator = LinearRegression()
# 使用fit方法进行训练
estimator.fit(x, y)
# 查看系数值
coef = estimator.coef_
print("系数值：", coef)  # 系数值： [0.3 0.7]

# 预测
print("预测值是：", estimator.predict([[90, 90]]))  # 预测值是： [90.]

三.线性回归的损失和优化

1.损失函数

又称最小二乘法

2.线性回归常用的优化算法

• 正规方程
• 梯度下降法

四.正规方程

1.介绍

2.正规方程的推导

利用矩阵的逆，转置进行一步求解，只适合样本和特征比较少的情况。

• 推导方式1：

• 推导方式2：

五.梯度下降(Gradient Descent)

1.概念

梯度下降的基本过程就和下山的场景类似。

首先，我们有一个 可微分的函数，这个函数就代表着一座山。

我们的目标就是找到 这个函数的最小值，也就是山底。

最快的下山方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走。对应到函数中，就是 找到给定点的梯度。然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数值变化最快的方向。所以我们反复利用这个方法，反复求取梯度，最后就能到达局部的最小值。

在单变量的函数中，梯度其实就是 函数的微分，代表着函数在某个给定点的切线的斜率。

在多变量的函数中，梯度是一个向量，向量有方向，梯度的方向就指出了给定点的上升最快的方向。

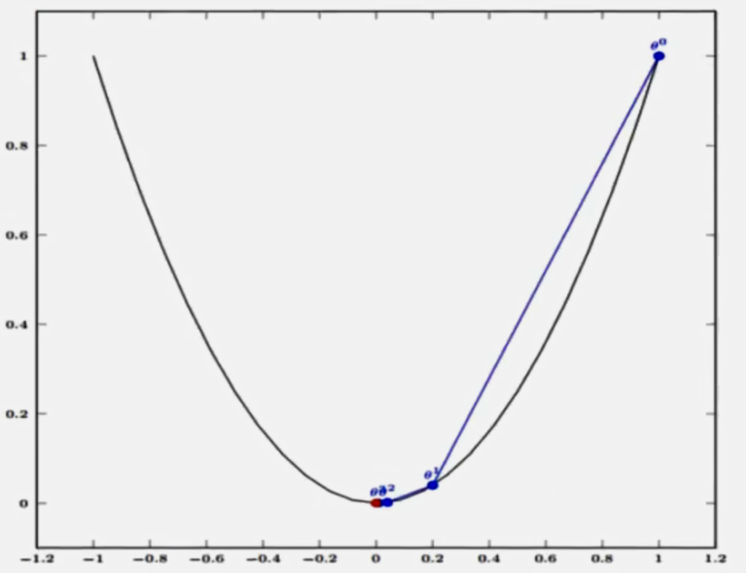
2.单变量函数的梯度下降

如下图，经过四次的运算，也就是走了4步，基本抵达了函数的最低点，也就是山底。

3.多变量函数的梯度下降

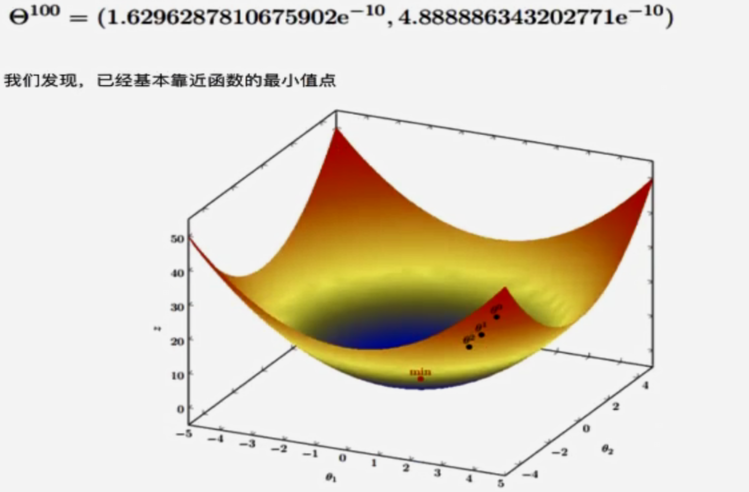
4.梯度下降公式

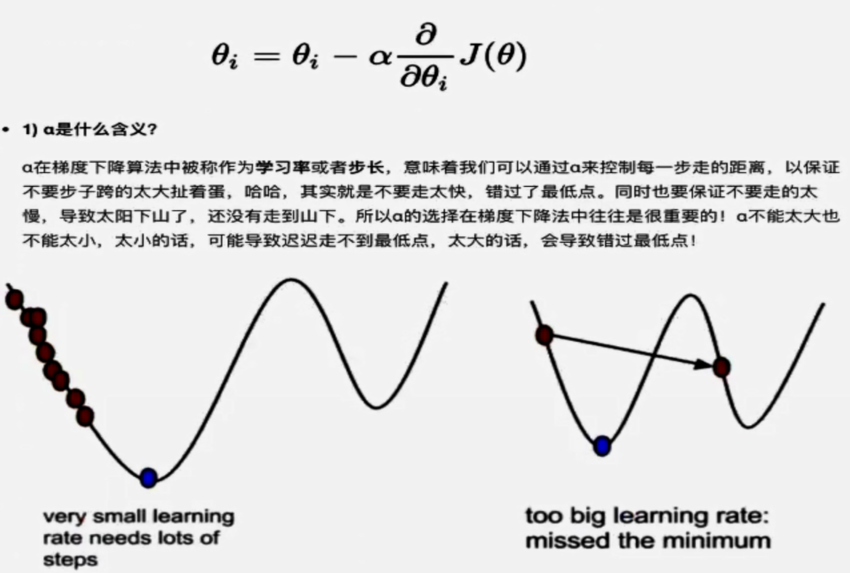
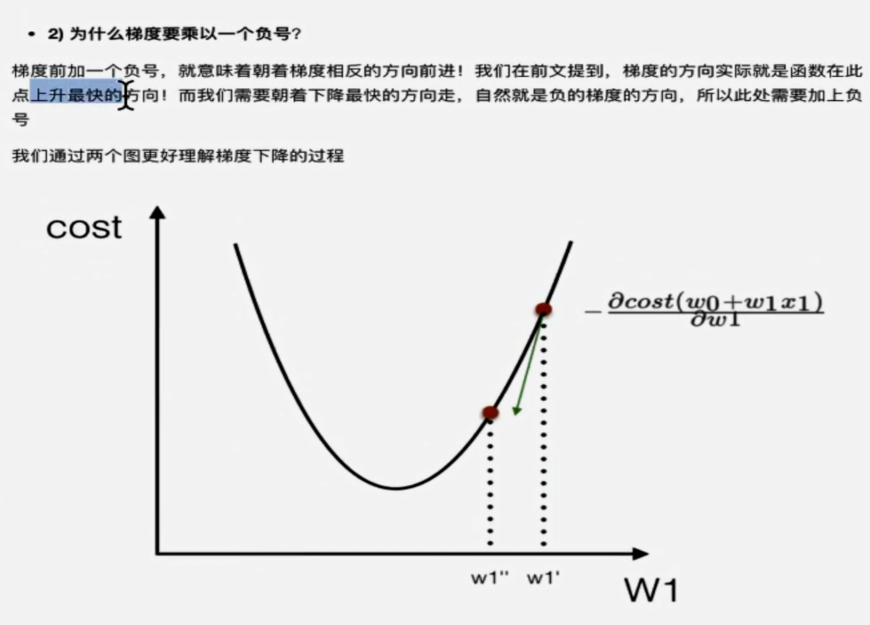
有了梯度下降这个优化算法，回归就有了“自动学习”的能力。但是梯度下降并不能保证我们找到的是最优解，即最小值。

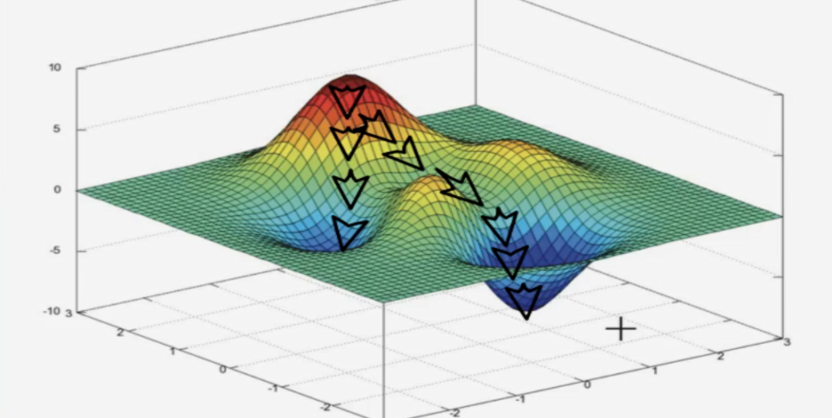
5.梯度下降和正规方程的对比

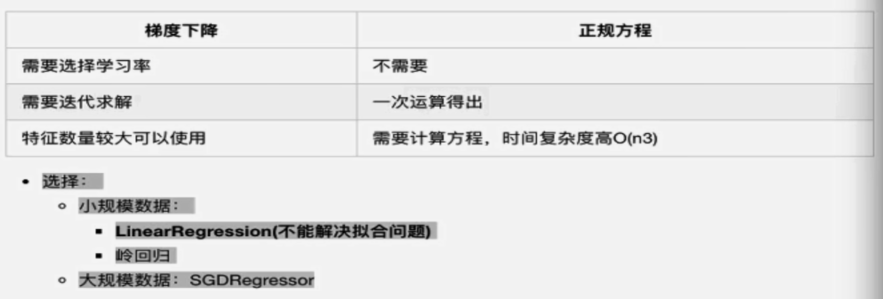
六.常见的梯度下降算法

• 全梯度下降算法(full gradient descent)
• 随机梯度下降算法(stochastic gradient descent)
• 随机平均梯度下降算法(stochastic average gradient descent)
• 小批量梯度下降算法(mini-batch gradient descent)

他们都是为了正确地调节权重向量，通过为每个权重计算一个梯度，从而更新权值，使目标函数尽可能最小化。其差别在于样本的使用方式不同。

1.全梯度下降算法（FG）

简言之，在进行计算的时候，计算所有样本的误差平均值，作为目标函数。

计算训练集所有样本误差，对其求和再取平均值作为目标函数。

权重向量沿其梯度相反的方向移动，从而使当前目标函数减少得最多。

因为在执行每次更新时，我们需要在整个数据集上计算所有的梯度，所以批梯度下降法的速度会很慢，同时，批梯度下降法无法处理超出内存容量限制的数据集。

批梯度下降法同样也不能在线更新模型，即在运行的过程中，不能增加新的样本。

其是在整个训练数据集上计算损失函数关于参数θ的梯度：

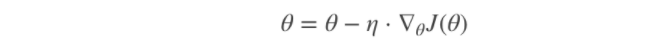
2.随机梯度下降算法（SG）

简言之，每次只选择一个样本进行考核。

由于FG每迭代更新一次权重都需要计算所有样本误差，而实际问题中经常有上亿的训练样本，故效率偏低，且容易陷入局部最优解，因此提出了随机梯度下降算法。

其每轮计算的目标函数不再是全体样本误差，而仅是单个样本误差，即 每次只代入计算一个样本目标函数的梯度 来更新权重，再取下一个样本重复此过程，直到损失函数值停止下降或损失函数值小于某个可以容忍的阈值。

此过程简单，高效，通常可以较好地避免更新迭代收敛到局部最优解。其迭代形式为

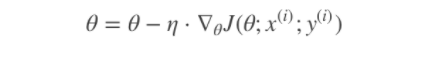
每次只使用一个样本迭代，若遇上噪声则容易陷入局部最优解。

其中，x(i)表示一条训练样本的特征值，y(i)表示一条训练样本的标签值

但是由于，SG每次只使用一个样本迭代，若遇上噪声则容易陷入局部最优解。

3.小批量梯度下降算法（mini-bantch）

小批量梯度下降算法是FG和SG的折中方案,在一定程度上兼顾了以上两种方法的优点。简言之，选择一小部分样本进行考核。

每次从训练样本集上随机抽取一个小样本集，在抽出来的小样本集上采用FG迭代更新权重。

被抽出的小样本集所含样本点的个数称为batch_size，通常设置为2的幂次方，更有利于GPU加速处理。

特别的，若batch_size=1，则变成了SG；若batch_size=n，则变成了FG.其迭代形式为

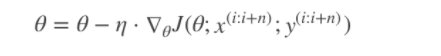
4.随机平均梯度下降算法（SAG）

简言之，会给每个样本都维持一个平均值，后期计算的时候，参考这个平均值。

在SG方法中，虽然避开了运算成本大的问题，但对于大数据训练而言，SG效果常不尽如人意，因为每一轮梯度更新都完全与上一轮的数据和梯度无关。

随机平均梯度算法克服了这个问题，在内存中 为每一个样本都维护一个旧的梯度，随机选择第i个样本来更新此样本的梯度，其他样本的梯度保持不变，然后求得所有梯度的平均值，进而更新了参数。

如此，每一轮更新仅需计算一个样本的梯度，计算成本等同于SG，但收敛速度快得多。

5.算法比较

为了比对四种基本梯度下降算法的性能，我们通过一个逻辑二分类实验来说明。

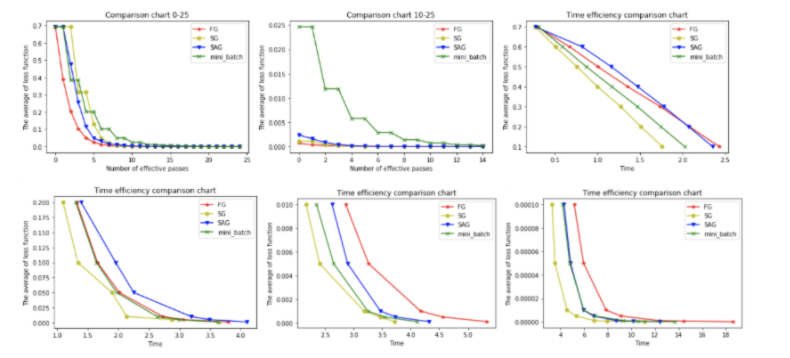
综合分析六幅图我们得出以下结论：

（1）FG方法由于它每轮更新都要使用全体数据集，故花费的时间成本最多，内存存储最大。

（2）SAG在训练初期表现不佳，优化速度较慢。这是因为我们常将初始梯度设为0，而SAG每轮梯度更新都结合了上一轮梯度值。

（3）综合考虑迭代次数和运行时间，SG表现性能都很好，能在训练初期快速摆脱初始梯度值，快速将平均损失函数降到很低。但要注意，在使用SG方法时要慎重选择步长，否则容易错过最优解。

（4）mini-batch结合了SG的“胆大”和FG的“心细”，从6幅图像来看，它的表现也正好居于SG和FG二者之间。在目前的机器学习领域，mini-batch是使用最多的梯度下降算法，正是因为它避开了FG运算效率低成本大和SG收敛效果不稳定的缺点。