一.概述

1.定义：

K-近邻算法，也叫KNN算法，是一种分类算法。指的是如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。通俗的说就是根据你的“邻居”来判断你属于哪个类别。

2.实现流程

• 计算已知类别数据集中的点与当前点之间的距离
• 按距离递增次序排序
• 选取与当前点距离最小的k个点
• 统计前k个点所在的类别出现的频率
• 返回前k个点出现频率最高的类别作为当前点的预测分类

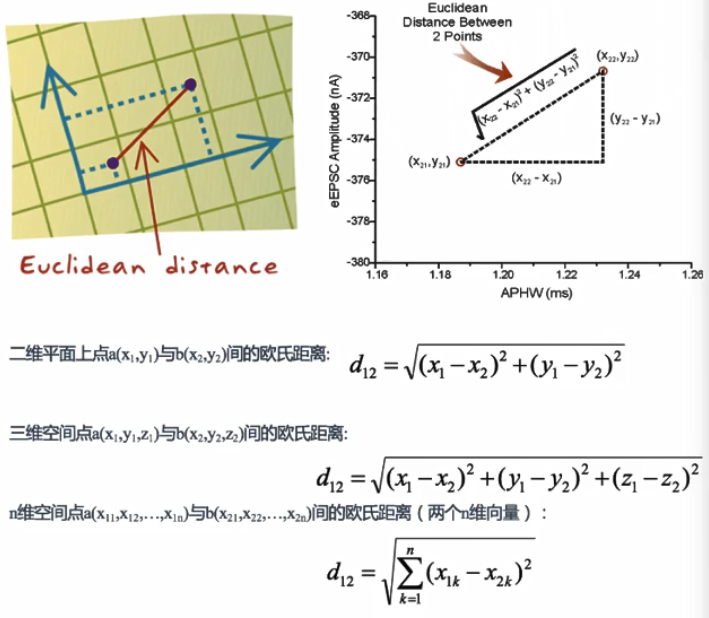
3.距离公式

如何计算你到你的“邻居”的距离 一般使用欧氏距离

二.Scikit-learn工具介绍

1.安装

pip3 install scikit-learn==0.19.1 

2.导入

import sklearn

注意 安装scikit-learn需要Numpy、pandas等库

3.优势

• 文档多，且规范
• 包含的算法多
• 实现起来容易

4.Scikit-learn包含的内容

三.K-近邻算法API初步使用

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)

# n_neighbors:int,可选（默认5），k_neighbors查询默认使用的邻居数

简单使用：

from sklearn.neighbors import KNeighborsClassifier

# 获取数据
x = [[1], [3], [7], [9]]
# 分为两个类别0，1
y = [1, 1, 0, 0]

# 机器学习
# 1.实例化一个训练模型
estimator = KNeighborsClassifier(n_neighbors=4)
# 2.调用fit方法进行训练
estimator.fit(x, y)

# 预测其他值，5的分类为[0]
ret = estimator.predict([[5]])
print(ret)

四.距离度量

1.欧式距离

通过距离平方值进行计算

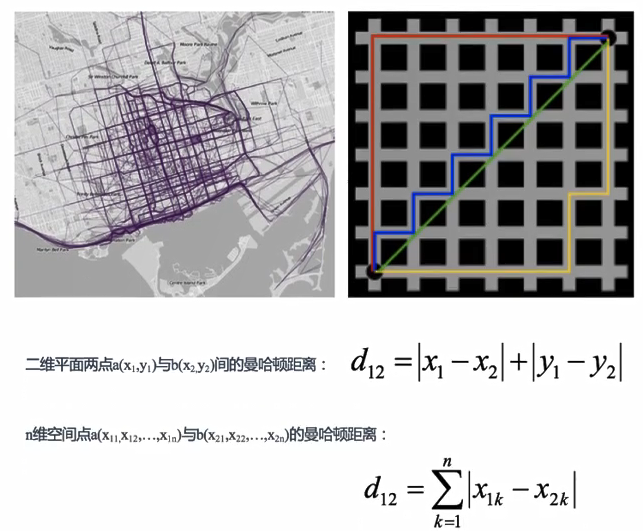
2.曼哈顿距离

曼哈顿距离也叫“城市街区距离”，通过距离的绝对值进行计算

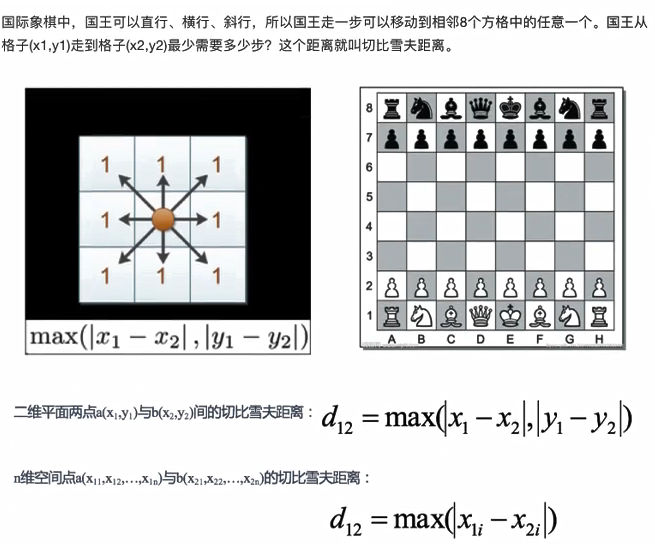
3.切比雪夫距离

维度的最大值进行计算

4.闵可夫斯基距离

闵可夫距离不是一种距离，是一组距离的定义，是对多个距离度量公式的概括性的表达。

前四个距离公式都是把单位相同看待了，所以计算过程不是很科学。

5.标准化欧氏距离

标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。思路是既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。

在计算过程中添加了标准差，对量纲数据进行处理。

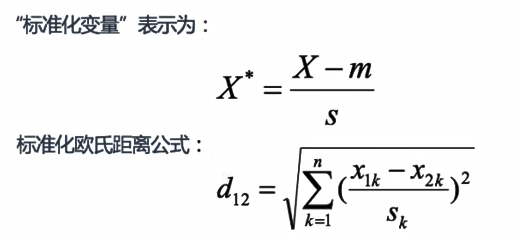
6.余弦距离

几何中，夹角余弦可用来衡量两个向量方向的差异，在机器学习中，借用这一概念来衡量样本向量之间的差异。

通过cos思想完成。

7.汗明距离

两个等长字符串s1与s2的汉明距离为：将其中一个变为另外一个所需要作的最小字符替换次数。

8.杰卡德距离

通过交并集进行统计

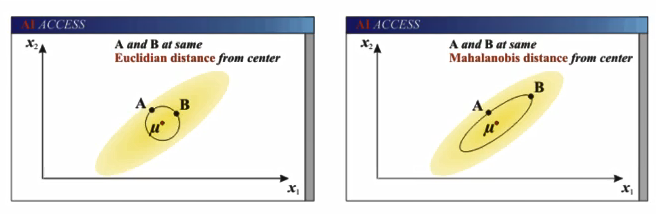
9.马氏距离

马氏距离是基于样本分布的一种距离，表示数据的协方差距离。他是一种有效的计算两个位置样本集的相似度的方法。

通过样本分布进行计算。

马氏距离特性：

1.量纲无关，排除变量之间的相关性的干扰

2.马氏距离的计算是建立在总体样本的基础上的

3.计算马氏距离的过程中，要求总体样本数大于样本的维数

欧氏距离&马氏距离

五.k值的选择

K值过小：容易收到异常点的影响，容易过拟合

K值过大：受到样本均衡的问题，容易欠拟合

K值的选择，李航博士的《统计学习方法》说：

近似误差：对现有训练集的训练误差，关注训练集，如果近似误差过小可能会出现过拟合的现象，对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。（训练集上表现好，测试集表现不好，容易过拟合）

估计误差：对测试集的测试误差，关注测试集，估计误差小说明对未知数据的预测能力好，模型本身最接近最佳模型。

六.kd树

1.kd树介绍

为什么需要kd树 ?

根据KNN每次需要预测一个点时，我们都需要计算数据集中每个点到这个点的距离，然后选出距离最近的k个点进行投票。当数据集很大时，这个计算成本非常高，针对N个样本，D个特征的数据集，其算法复杂度为O（DN^2）

kd树是什么 ？

为了避免每次都重新计算一遍距离，算法会把距离信息保存在一颗树里。其基本原理是：如果A和B距离很远，B和C距离很近，那么A和C距离也很远。有了这个信息，就可以在合适的时候跳过距离远的点。这样优化后的算法复杂度可降低到O（DNLog(N)）。

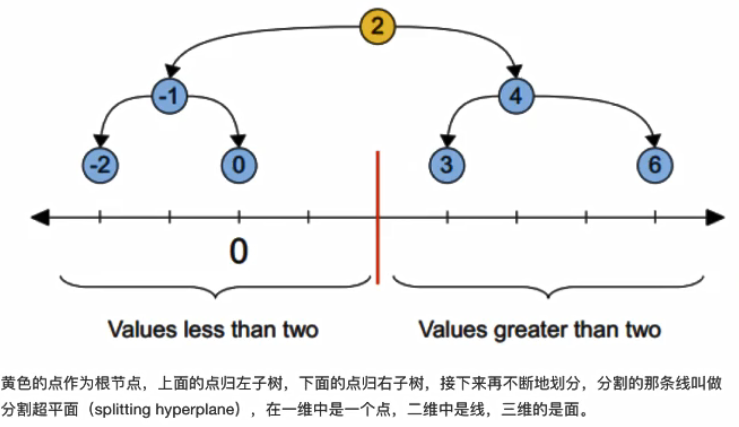
2.kd数构造方法

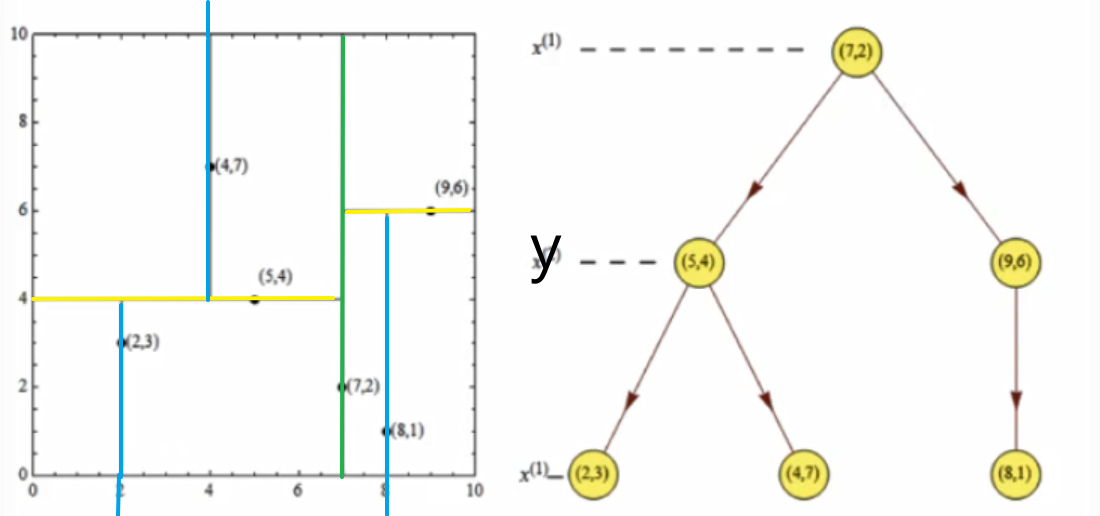
给定一个二维空间数据集：T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},构造一个平衡kd树。

第一次:
x轴-- 2,5,9,4,8,7 --> 2,4,5,7,8,9
y轴-- 3,4,6,7,1,2 --> 1,2,3,4,6,7

首先选择x轴, 找中间点,发现是(7,2)

第二次:
左面: (2,3), [4,7], [5,4] --> 3,4,7
右面: (8,1), (9,6) --> 1,6

从y轴开始选择, 左边选择点是(5,4),右边选择点(9,6)

第三次:
从x轴开始选择

3.最近邻域搜索

kd树是一种对k维空间中的示例点进行存储以便对其进行快速检索的树形数据结构。

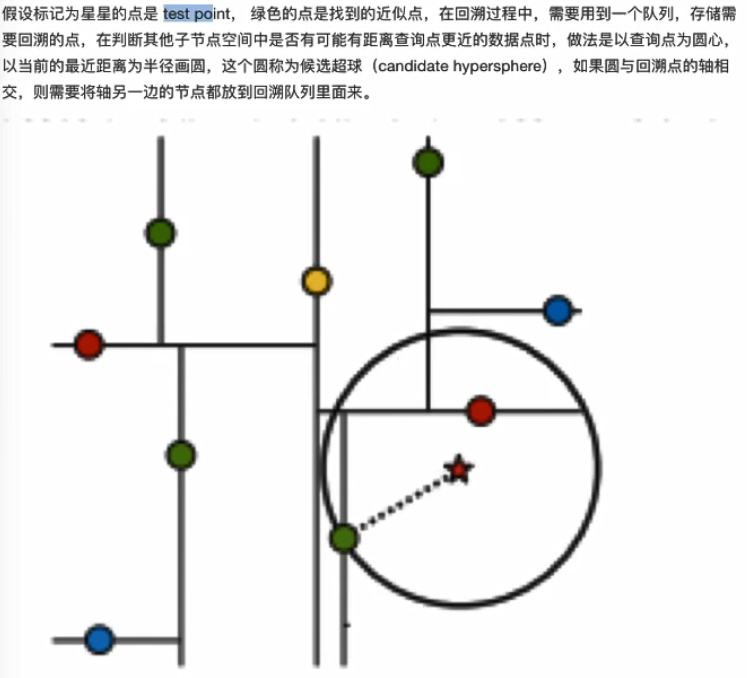
样本集T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}

3.1 查找点（2.1，3.1）

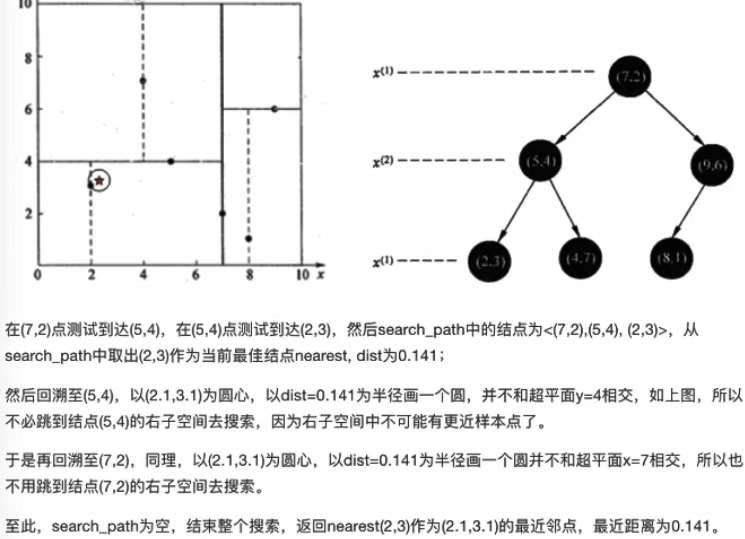
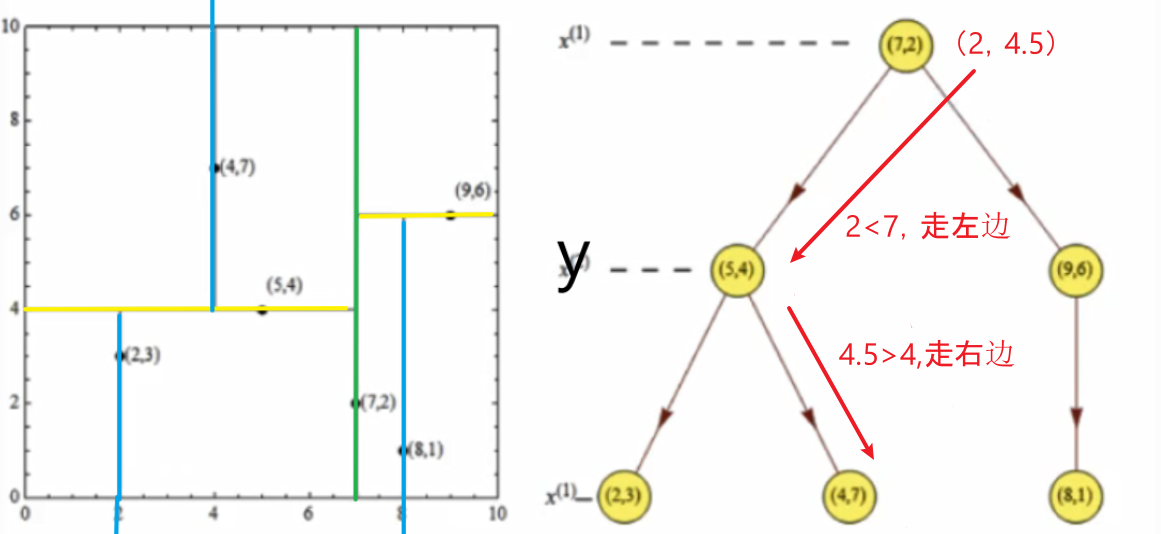
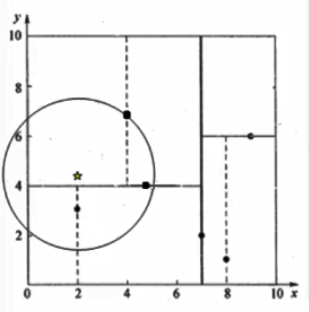
3.2 查找点（2，4.5）

七.k近邻算法总结

1.优点

• 简单有效
• 重新训练的代价低
• 适合类域交叉样本

主要靠周围有限的邻近样本，而不是靠判别类域的方法确定所属类别，因此对于类域的交叉或者重叠较多的待分样本集来说，KNN较其他方法更为合适。

• 适合大样本自动分类

比较适用于样本容量比较大的类域的自动分类，而那些样本容易较小的类域采用这种算法比较容易产生误分。

2.缺点

• 惰性学习

• 类别评分不是规格化

不像一些通过概率评分的分类

• 输出可解释性不强

例如决策树的输出可解释性就较强

• 对不均衡的样本不擅长

（1）可以重新采集样本；

（2）也可以采用权值的方法（和该样本距离小的邻居权值大）来改进。

• 计算量较大

目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。