机器学习系列04丨常用科学计算库的使用 Numpy

2021-07-12 | 阅读：次

一.什么是Numpy

Numpy（Numerical Python）是一个开源的Python科学计算库，用于快速处理任意维度的数组。Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务，使用Numpy比直接使用Python要简洁的多。Numpy使用ndarray对象来处理多维数组，该对象是一个快速而灵活的大数据容器。

二.ndarray与Python原生list运算效率对比

import random
import time
import numpy as np

a = []
for i in range(100000000):
    a.append(random.random())

1.python原生list运算

通过%time魔法方法，查看当前行的代码运行一次所花费的时间

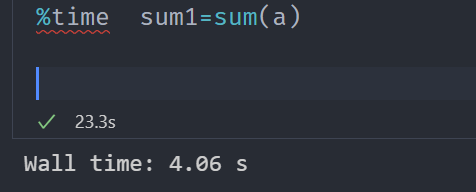
%time  sum1=sum(a)

使用原生Python计算时间的结果如下图，4.06s

20210811165300

2.使用ndarray运算方法

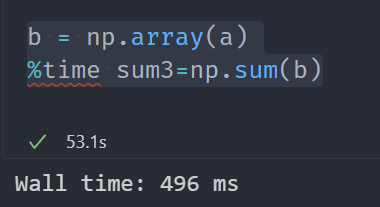
b = np.array(a)
%time sum3=np.sum(b)

使用ndarray的结果如下图,496ms，从中我们看到ndarray的计算速度要快很多，节约了时间。

20210811165645

Numpy专门针对ndarray的操作和运算进行了设计，所以数组的存储效率和输入输出性能远优于Python中的嵌套列表，数组越大，Numpy的优势就越明显。

三.ndarray的优势

1.内存块风格

ndarray存储数据的时候，数据与数据的地址都是连续的，这样使得批量操作数据元素时速度更快

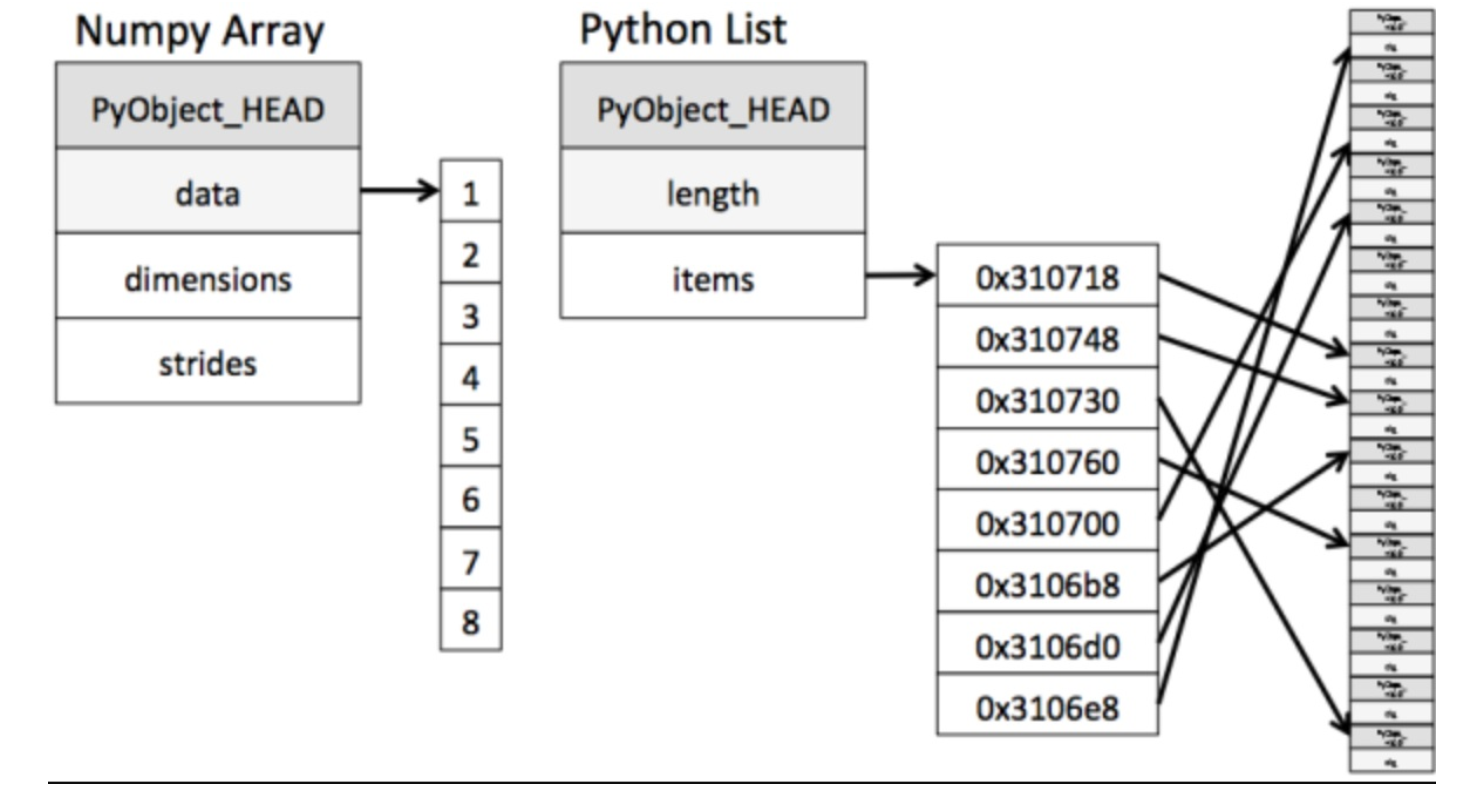
20210811170249

从图中可以看出ndarray在存储数据的时候，数据与数据的地址都是连续的，这样就给使得批量操作数组元素时速度更快。这是因为ndarray中的所有元素的类型都是相同的，而Python列表中的元素类型是任意的，所以ndarray在存储元素时内存可以连续，而python原生list就只能通过寻址方式找到下一个元素。

2.ndarray支持并行化运算

numpy内置了并行运算功能，当系统有多个核心时，做某种运算时numpy会自动做并行计算

3.效率远高于纯python代码

numpy底层用C语言编写，内部解除了GIL(全局解释器锁)，对数组的操作速度不受python解释器限制，所以效率高于纯python代码。

四.数组的属性、形状、类型

1.数组的属性

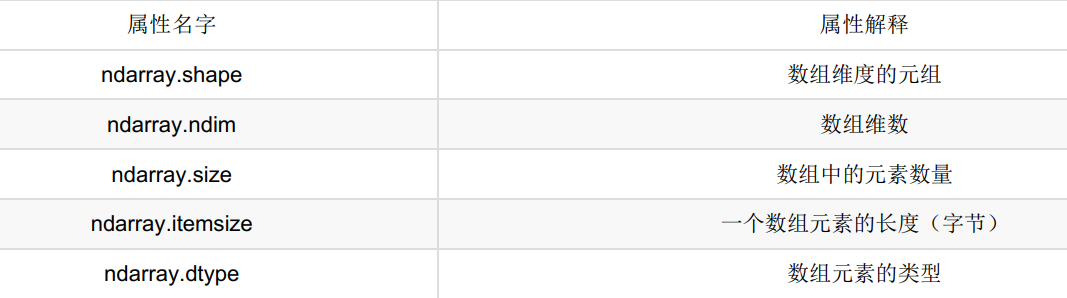
20210811171156

查看数组的属性信息

score = np.array([
    [12,3,4,5],
    [14,5,68,8],
    [46,89,6,432]
])
# 数组维度的元组  三行四列(3, 4)
score.shape

# 数组维数   2
score.ndim

# 数组中的元素数量  12
score.size  

# 一个数组元素的长度(字节)  4
score.itemsize

# 数组元素的类型  dtype('int32')
score.dtype 

2.数组的形状

# 一维数组
a = np.array([2,4,5,6])
a
a.shape

# 二维数组
b = np.array([
    [1,4,6],
    [4,66,2]
])
b
b.shape

# 三维数组
c = np.array([
[
    [1,4,6],
    [4,66,2]
],
[
    [2,43,3],
    [1,3,24]
],

])
c
c.shape   # (2, 2, 3) 第一个2是有两个二维数组，第二个2是每个二维数组中有两个一维数组，3是每个一维数组有3个元素

3.数组的类型

# 指定类型为浮点型
b = np.array([[1,4,6],[4,66,2]],dtype=np.float32)
b

# 指定字符串类型
arr = np.array(["python,tf,touch"],dtype=np.string_)
arr  #array([b'python,tf,touch'], dtype='|S15' 15代表字符串长度

五.数组的基本操作

1.生成数组的方式

1.1 生成 0 1 数组

ones = np.ones([3,2])  # 3行2列
ones
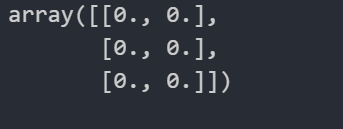
np.zeros_like(ones)  # 变为全0

结果如下：

20210811172228

1.2从现有数组生成

a = np.array([[1,34,5],[4,65,3]])
a

1.2.1 比较array和asarray区别

a1 = np.array(a)    # 深拷贝
a1

a2 = np.asarray(a)  # 浅拷贝
a2

# 修改第一个数组第一个元素为1000
a[0,0] = 1000

# array方法还是1
a1  # 第一个数组第一个元素为1

# asarray方法
a2  # 第一个数组第一个元素为1000

1.3生成固定范围的数组

# 从0-40生成5个数
np.linspace(0,40,5)  #array([ 0., 10., 20., 30., 40.])

# 创建等差数组-指定步长  从10-60，步长为5生成数据
np.arange(10,60,5)  #array([10, 15, 20, 25, 30, 35, 40, 45, 50, 55])

# 创建等比数列   生成10^x
np.logspace(0,2,3) #array([  1.,  10., 100.]) 

1.4生成随机数组

import matplotlib.pyplot as plt
#生成均值1.75，标准差为1的正态分布数据，100000000个
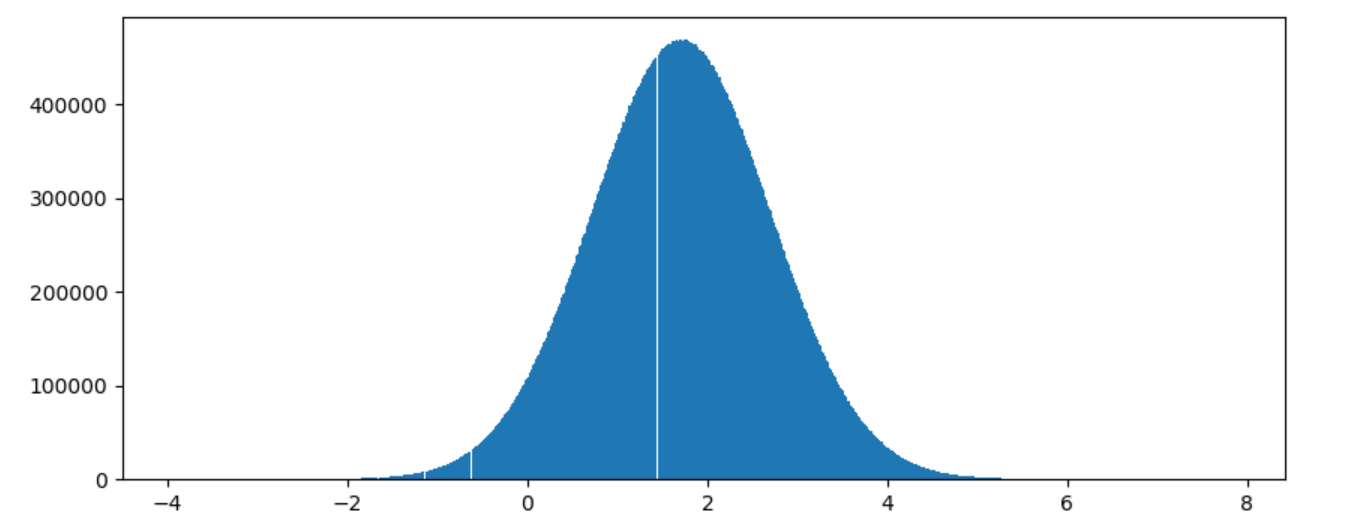
x1 = np.random.normal(1.71,1,100000000)
print(x1)  #[0.37338478 1.47709387 1.40373188 ... 1.54515649 1.50143846 2.03444761]
#画图看分布状况
#创建画布
plt.figure(figsize=(10,4),dpi=100)
# 绘制直方图
plt.hist(x1,1000)

plt.savefig("./pic2.png")
#显示图像
plt.show()

20210811174729

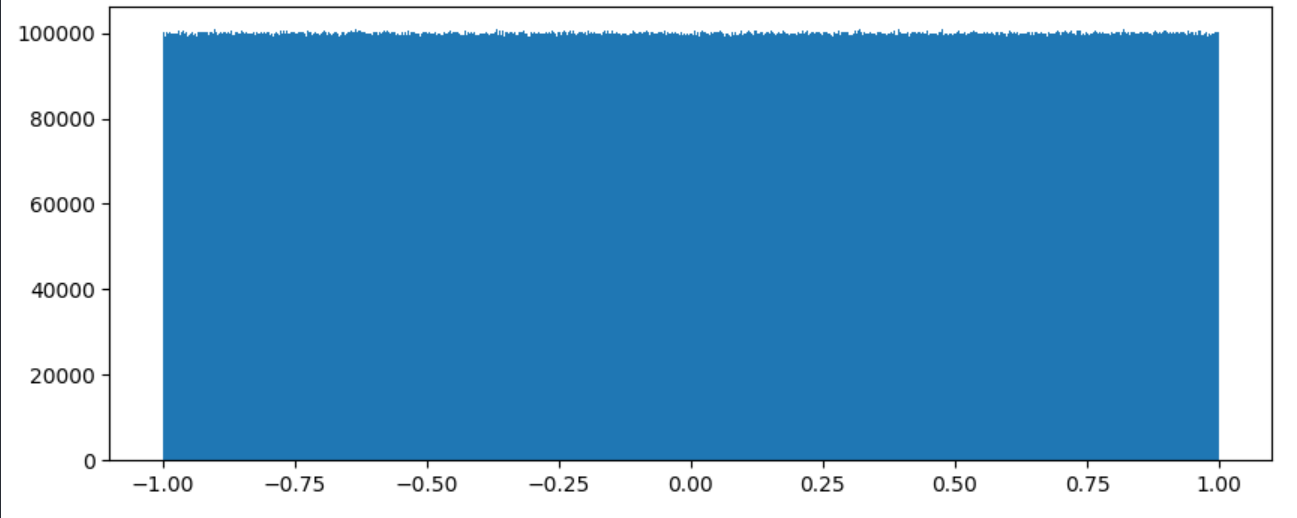
2. 均匀分布

# 下界-1，上界为1，生成均匀分布的随机数
x2 = np.random.uniform(-1,1,100000000)
x2
# 画图看分布状况
# 1）创建画布
plt.figure(figsize=(10,4),dpi=100)
# 2）绘制直方图，分成1000组
plt.hist(x2,1000)
# 3）显示图像
plt.show()

20210811174936

3. 数组的索引、切片

3.1 取数

import numpy as np

a = ([
    [[1,4,5],[2,3,4]],
    [[4,5,76],[2,4,6]],
])

# 取出第1个二维数组的第1个数组的第2个元素  
a[1][1][2]   # 6

3.2 数组的去重

import numpy as np
a = np.array([[1,3,4],[3,5,7]])
a
np.unique(a)   #array([1, 3, 4, 5, 7])

4. ndarray运算

4.1 逻辑运算

import numpy as np
# 40-100之间的数，10行5列
score = np.random.randint(40,100,(10,5))
score
# 取出从第六行开始，每行的0-2列
test_score = score[6:,0:3]
test_score
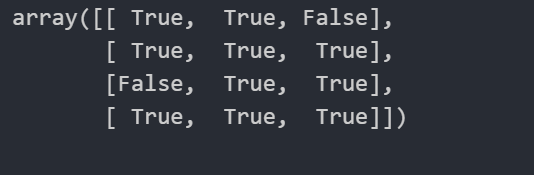
# 查看元素是否大于60
test_score > 60

20210811181014

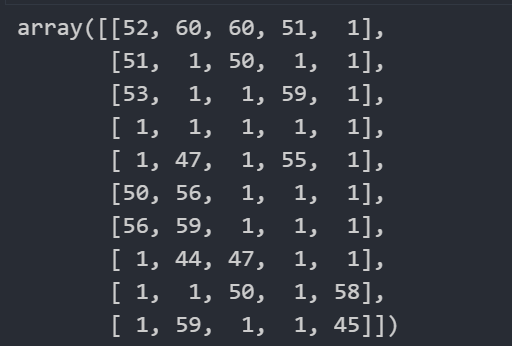
score = np.random.randint(40,100,(10,5))
# 大于60的赋值为1
score[score > 60] = 1
score

20210811181101

4.2 通用判断函数

np.all 都满足才返回True

# 前两个同学的所有科目
score = np.random.randint(40,100,(10,5))
test_score = np.all(score[0:2,:] >60)
test_score
score

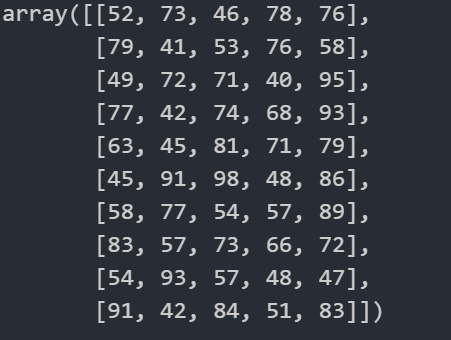
20210811181217

np.any 判断有任意满足条件返回True

test_score = np.any(score[0:2,:] > 70)
test_score # True

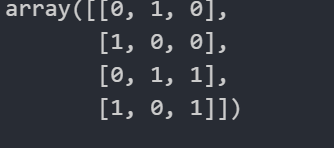
np.where 三元运算符

# 取前4名学生的前三门课
temp= score[0:4,0:3]
# 成绩大于60置为1，否则0
np.where(temp > 60,1,0)

20210811181432

4.3 统计运算

temp= score[:4,:]
temp
#array([[52, 73, 46, 78, 76],
#        [79, 41, 53, 76, 58],
#        [49, 72, 71, 40, 95],
#        [77, 42, 74, 68, 93]])

# 取最大的元素
np.max(temp)  # 95
# 取平均值
np.mean(temp) # 65.65
# 每列的最大值
np.max(temp,axis=0)  # array([79, 73, 74, 78, 95])
# 每行的最大值
np.max(temp,axis=1)  # array([78, 79, 95, 93])
# 最大值所在位置是第14个元素
np.argmax(temp) #14
# 每列最大值所在位置
np.argmax(temp,axis=0) #array([1, 0, 3, 0, 2], dtype=int64)

5. 数组间的运算

5.1数组与数的运算

a = np.array([[1,3,4],[5,7,8]])
# 每个元素都 + 3
print(a + 3)

b = ([1,3,5])
print(b * 3)  #[1, 3, 5, 1, 3, 5, 1, 3, 5]

5.2数组与数组的运算,要满足广播机制：

# (1) 数组中的某一维度等长
# (2) 其中一个数组的某一维度为1

arr1 = np.array([[1,2,3,4,5,5],[1,2,3,4,5,6]])   # 两行6列
arr2 = np.array([[1],[3]])  # 两行1列
print(arr1 + arr2)

5.3矩阵的运算

矩阵乘法遵循准则：

(M行N列)*(N行L列)=(M行,L列)

x1 = np.array([
    [80,32],
    [34,67],
    [36,74]
])

x2 = np.array([[3],[1]])
print(np.dot(x1,x2))
# [[272]
#  [169]
#  [182]]
print(np.matmul(x1,x2))
# [[272]
#  [169]
#  [182]]
x3 = 10
print(np.dot(x3,x1))
# [[800 320]
#  [340 670]
#  [360 740]]
print(np.matmul(x3,x1))  # matmul不支持矩阵和标量的乘法

Dylan

Kang Yaoming